Net Present Value (NPV) and Discounted Cash Flow Analysis (DCF) are financial/MBA wonky terms that may intimidate a majority of people. But in actuality they are simple concepts to understand. Once you realize that a dollar received in the future is worth less than a dollar received in the present, you’re halfway home.
In the words of Benjamin Franklin, “One today is worth two tomorrow.”
Why Should You Care?
The basics of NPV and DCF are not just applicable to CFOs and financial analysts, they’re also applicable to the small business deciding whether to purchase additional equipment, or the person deciding whether to lend money to a friend. These tools help you determine if an investment is profitable considering the time value of money.
If someone offers you $10,000 today, you can immediately invest that $10K in order to start earning money. If someone offers you the same $10,000 one year from now, you have missed a year’s worth of time to take that money and start earning interest.
What is the Discount Rate?
Consider if you will the concept of a “discount” interest rate. If you take your cash and simply invest it at this “discount” rate, you will have earned some return.
What is the discount rate you ask? The discount rate (or r) is the minimum rate of return that you require of an investment in order to take action.
- For example, you believe that $10,000 invested in the stock market today will offer you a 10% return in one year’s time (i.e. $1000)
- In order for you to consider an alternative option for investing your $10,000, it has to at least return greater than $1,000 in profit (i.e. return higher than the discount rate that you have established)
A Discount Metaphor
In this example, think of money as a collection of items from a high end clothing line that you are considering purchasing. If you buy the clothes today at present value, you are fine with the current price. But if someone tries to offer you the exact same set of clothes 1 year in the future for today’s prices, you would demand a discount to compensate for the indignity of wearing outdated clothes.
You might have paid $200 for a pair of Jordache jeans and a Member’s Only jacket in 1982, but if someone offered you those items for the same price 36 years later, you would demand a steep discount to compensate for the passage of time. Similar to cash received at a future date, the clothes are valued less the more years you move into the future.

Are you still a member?
Receiving $10,000 5 years in the future is not the same as receiving $10,000 today. You would need to discount that $10,000 future payment to reflect the passage of time. Applying your selected discount rate of 10% to the $10,000 received 5 years in the future, you would value that money at $6,209.21; i.e. $10,000/(1+0.1)^5. Don’t worry about the math yet.
If someone ever asks you for a $10,000 investment today only to repay you $10,000 in 5 years, please decline because you would be losing money. The $10K received 5 years in the future would be identical to $6,209 received today. This is because you can immediately invest the $6,209 today and let it compound for 5 years at 10% per year, and have the same $10K in 5 years’ time. Hopefully I haven’t lost you.
Here Comes the Math, Don’t be Scared:
Present Value Example:
- $10,000 in Present Value * 1.1 = Future Value of $11,000
- This is the same as saying that $10,000 today returning 10% interest is worth $11,000 in one year
Alternatively, to reverse the scenario:
- $11,000 in Future Value / (1+0.1) = Present Value of $10,000
- This is the same as saying that $11,000 received in one year has a present value of $10,000 at 10% interest
In both scenarios, receiving $11,000 in one year would be identical to having $10,000 today. Like those 80’s Members Only jackets, you are essentially applying a 10% discount off of the $11,000 received one year in the future, in order to value those future dollars in present terms.

FV = future cash to be received in year n
This formula is simply plug and chug. Remember that FV = the dollars you expect to receive at some point in the future (i.e. a future cash flow).
Years
You don’t have to limit yourself to evaluating a cash flow one year in the future. The variable n is used in this formula to represent the number of years in the future that you wish to evaluate money received.
Present Value with Years:
- $10,000 in Present Value * 1.1 * 1.1 = Future Value of $12,100 in two years’ time.
- This could also be expressed as $10,000 * (1.1)^2 = $12,100 where 2 represents the number of years in the future.
This is the same as saying that $10,000 today at 10% interest is worth $12,100 in two years.
Alternatively, to reverse the scenario:
- $12,100 in Future value / (1+0.1) / (1+0.1) = Present Value of $10,000.
- This could also be expressed as $12,100 / (1+0.1)^2 = Present value of $10,000
This is the same as saying that $12,100 received in two years has a present value of $10,000 today at 10% interest.
Net Present Value Scenario (Rolling in NPVs)
Now that you have an understanding of Present and Future Value, we can broach the concept of Discounted Cash Flow analysis or DCF. Again, don’t let the fancy wording intimidate you. This is simply a way of applying the Present Value formula we learned above to multiple cash flows (i.e. money that you receive at different years in the future).
Suppose that you are a financial analyst at the very prestigious Wu-Tang Financial investment firm. At this firm, cash rules everything around you so you have to make the right decisions in order to maintain your job. The firm is considering the following option in regards to investing its money and they’ve come to you for a breakdown of the analysis after firing the last financial analyst.
- Option 1: The firm is considering investing $10K in a Brooklyn Zoo. This option requires a $10K upfront investment and pays out cash flows as follows over the course of 5 years
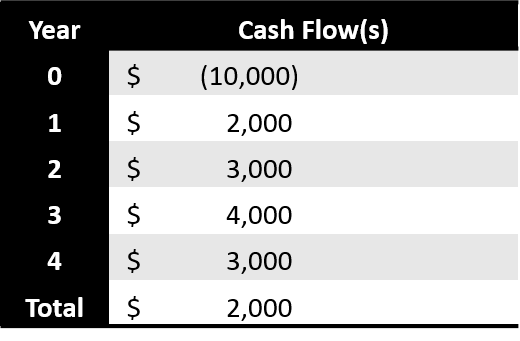
In our example, the firm invests $10K today (i.e Year 0) and receives $2K in one year, $3K in two years, $4K in 3 years and a final payment of $3k in 4 years’ time. The initial $10K investment is represented as a negative number to indicate that it is a payment and those funds are no longer available to the investor.
The previous financial analyst would have simply added all of the cash flows together and determined if the sum of those cash flows were positive. He would have recommended that the firm move forward with the Brooklyn Zoo investment because it returned $2K to the firm over the course of 4 years.
You immediately recognized that this approach does not consider the time value of money. You determine that if the firm were to simply diversify its bonds, it could earn an easy 10% per year on that initial $10K investment. You choose 10% as your discount rate and protect your neck by applying a discounted cash flow analysis.
You proceed to calculate the present value of all of the expected cash flows in the year that they are expected.

With an NPV of -$648.18, this investment is a money loser
By taking the Cash Flow numbers in column B and individually dividing them by (1+.01)^Year, (where .01 represents the 10% discount rate) you were able to calculate the present value (column D) of all the cash flows by the year in which they were received.
For example, the expected $2,000 received in Year 2 is only worth $1,818.18 today. That’s because $1818.18 invested today at 10% interest will produce $2,000 in one year. This same concept applies to the cash flows represented for each year.
By adding and subtracting all of the present values in column D, you’ve calculated the Net Present Value of the Brooklyn Zoo investment (considering you could have earned 10% compounded yearly in an alternate investment).

When calculating NPV, initial investment is typically a negative number
By evaluating the investment in this manner, you’ve easily determined that a potential investment in the Brooklyn Zoo would lead to a loss of $648.18. If the firm were to simply take that initial $10K and collect 10% interest per year compounded for 4 years, it would have collected an additional $648.18 in profit.
You decide to tell management “Shame on you if you move forward with this investment.”
Summary
Hopefully if you made it this far, the following summary will make sense. If you need to analyze the profitability of a potential investment, take the following steps:
- Pick an interest rate as your “discount rate”. Investing your dollars at this rate of return will always be your default fallback option
- The discount rate (or r) is the minimum rate of return that you require of an investment in order to take action
- Calculate the Present Value of all cash flows received in the future (i.e. Future Value) with the following formula:

- This method is known as a Discounted Cash Flow analysis. Summing all of the Present Values of Future Cash Flows determines the Net Present Value (NPV) of the investment
- If the NPV returns a positive number, then this initiative should be pursued as it provides value over and above dollars invested at the discount rate of return
- If the NPV returns a negative number, then the initiative should not be pursued as it subtracts value in comparison to the same dollars invested at the discount rate of return. You should instead invest your dollars at your initial discount rate.
Tableau NPV Dashboard
If you follow my blog, you know Tableau has to figure in to my post somehow. Here is the sample dashboard used at Wu-Tang Financial to present the results of our Brooklyn Zoo NPV case. The bar chart discounted values or present values are highlighted in yellow (e.g. $1.8K, $2.5K, etc.), while the expected future cash flows are a muted color and labeled above the present values. As you change the Discount Rate Parameter slide, the NPV is recalculated and the bar charts are updated.
Feel free to download and/or interact with it on Tableau Public.
Always remember, as with any analysis, the results are only as good as the inputs!
Header Image Copyright: photonphoto / 123RF Stock Photo


